OPERASI KOMPOSISI DAN OPERASI INVERS PADA FUNGSI
PENGANTAR :
Modul ini kami susun sebagai salah satu sumber belajar untuk siswa agar dapat dipelajari dengan lebih mudah. Kami menyajikan materi dalam modul ini berusaha mengacu pada pendekatan kontekstual dengan diharapkan matematika akan makin terasa kegunaannya dalam kehidupan sehari-hari.
STANDAR KOMPETENSI : 5. Menentukan komposisi dua fungsi dan invers suatu
fungsi.
KOMPETENSI DASAR : 5.1 Menentukan komposisi fungsi dari dua fungsi
5.2 Menentukan invers suatu fungsi
TUJUAN PEMBELAJARAN :
1. Menentukan syarat dan aturan fungsi yang dapat dikomposisikan
2. Menentukan fungsi komposisi dari beberapa fungsi.
3. Menyebutkan sifat-sifat komposisi fungsi.
4. Menentukan komponen pembentuk fungsi komposisi apabila fungsi komposisi dan komponen lainnya diketahui.
5. Menjelaskan syarat agar suatu fungsi mempunyai invers.
6. Menggambarkan grafik fungsi invers dari grafik fungsi asalnya
7. Menentukan fungsi invers dari suatu fungsi.
8. mengidentifikasi sifat-sifat fungsi invers.
KEGIATAN BELAJAR :
I. Judul sub kegiatan belajar :
1. Pengertian Fungsi
2. Komposisi Fungsi
3. Sifat-sifat Komposisi Fungsi
4. Fungsi invers
II. Uraian materi dan contoh
1. Pengertian Fungsi
Definisi : Fungsi dari himpunan A ke himpunan B suatu relasi sedemikian hingga setiap anggota himpunan A dipasangkan dengan tepat satu anggota himpunan B.
Domain = daerah asal (D)
Kodomain = daerah kawan (K)
Range = daerah hasil (R)
![]() Notasi
Fungsi
Notasi
Fungsi
Suatu fungsi atau pemetaanumumnya dinotasikan denganhuruf kecil.
Misal, f adalah fungsi dari A ke Bditulis f: A → B
A disebut domain
B disebut kodomain
![]() Range atau
Daerah Hasil Jika f memetakan x Î A ke y Î B dikatakan y adalah
Range atau
Daerah Hasil Jika f memetakan x Î A ke y Î B dikatakan y adalah
peta dari x ditulis f: x → y atau y = f(x).
Himpunan y Î B yang merupakan peta dari x Î A
disebut range atau daerah hasil
Contoh 1
Misal f: R → R dengan f(x) = √1 - x2
Tentukan domain dari fungsi f.
Jawab
Supaya f: R→R dengan f(x)=√1-x2 maka haruslah 1 – x2 ≥ 0.
1 – x2 ≥ 0 → x2 – 1 ≤ 0 atau (x - 1)(x + 1) ≤ 0 atau -1 ≤ x ≤ 1.
Jadi, domain fungsi tersebut adalah -1 ≤ x ≤ 1.
Contoh 2
Misal f: R → R dengan f(x – 1) = x2 + 5x
Tentukan : a. f(x)
b. f(-3)
Jawab
Misal y = x – 1 maka x = y + 1
karena f(x – 1) = x2 + 5x
maka f(y) = (y + 1)2 + 5(y + 1)
f(y) = y2 + 2y + 1 + 5y + 5
f(y) = y2 + 7y + 6
f(y) = y2 + 7y + 6
a. f(x) = x2 + 7x + 6
b. f(-3) = (-3)2 + 7(-3) + 6
= 9 – 21 + 6
= -6
Contoh 3:
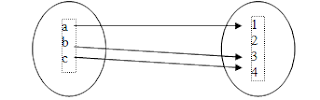
![]() Fungsi f : A B
tentukan domain, kodomain dan range
Fungsi f : A B
tentukan domain, kodomain dan range
Domain = {a,b,c}
Kodomain = {1,2,3,4}
Range = {1,3,4}
2. Komposisi Fungsi
Pengertian
Komposisi fungsi adalah penggabungan operasi dua fungsi secara berurutan sehingga menghasilkan sebuah fungsi baru.
Misalkan: f : A ® B dan g : B ® C
Fungsi baru h = (g o f) : A ® C disebut fungsi komposisi dari f dan g.
Ditulis: h(x) = (gof)(x) = g(f(x))
Nilai fungsi komposisi (gof)(x) untuk x = a adalah (gof)(a) = g(f(a))
Contoh 1:
Diketahui fungsi f dan g dinyatakan dalam pasangan terurut
f = {(0,1), (2,4), (3,-1),(4,5)} dan g = {(2,0), (1,2), (5,3), (6,7)}
Tentukanlah: a) (f o g) b) (g o f) c) (f o g)(1) d) (g o f)(4)
Jawab:
a) (f o g) = {(2,1), (1,4), (5,-1)} b) (g o f) = {(0,2), (4,3)}
c) (f o g)(1) = 4 d) (g o f)(4) = 3
Contoh 2:
f : R ® R ; f(x) = 2x² +1, g : R ® R ; g(x) = x + 3
Tentukan : a) (f o g)(x) b) (g o f)(x) c) (f o g)(1) d) (g o f)(1)
Jawab :
(f o g)(x) = f(g(x))
= f(x+3)
= 2(x+3)²+1
= 2(x² + 6x + 9) + 1
= 2x²+12x+19
(g o f)(x) = g(f(x))
= g(2x²+1)
= 2x² + 1 + 3
= 2x² + 4
(f o g)(1) = f(g(1))
= f(4)
= 2. (4)² +1
= 2.16 + 1
= 33
(g o f)(1) = g(f(1))
= g(3)
= 3 + 3
= 6
Contoh 3:
Diketahui A = {x l x < -1}, B dan C adalah himpunan bilangan real.
f : A → B dengan f(x) = -x + 1; g : B → C dengan g(x) = x2 dan
h = g o f : A → C.
Bila x di A dipetakan ke 64 di C, tentukan nilai x!
h(x) = (g o f)(x) = g(f(x)) = g(-x + 1) = (-x + 1)2
h(x) = 64 → (-x + 1)2 = 64 ↔ -x + 1 = ± 8
-x + 1 = 8 ↔ x = -7 atau –x + 1 = -8 ↔ x = 9
Karena A = {x l x < -1}, maka nilai x yang memenuhi adalah x = -7.
3. Sifat-sifat Komposisi Fungsi
Contoh 4:
Diketahui f(x) = 2x + 1, g(x) = 3 – x, dan h(x) = x2 + 2, I(x) = x
(f o g)(x) = f(g(x)) = f(3-x) = 2(3-x) + 1 = 6 – 2x + 1 = 7 – 2x
(g o f)(x) = g(f(x)) = g(2x+1) = 3 – (2x+1) = 3 – 2x – 1 = 2 – 2x
(g o h)(x) = g(h(x)) = g(x2 + 2) = 3 – (x2 + 2) = 1 - x2
Dari hasil di atas tampak bahwa (fog)(x) ≠ (g o f)(x)
((fog)oh)(x) = (fog)(h(x))= (fog)( x2 + 2)= 7 – 2(x2 + 2) = 3 - 2x2
(fo(goh))(x)=f((goh)(x))= f(1 - x2)= 2(1 - x2) + 1 = 2 – 2 x2 + 1 = 3 – 2 x2
Dari hasil di atas tampak bahwa ((fog)oh)(x) = (fo(goh))(x)
(foI)(x) = f(I(x)) = f(x) = 2x + 1
(Iof)(x) = I(f(x)) = I(2x+1) = 2x + 1
Dari hasil di atas tampak bahwa (foI)(x) = (Iof)(x) = f(x)
4. Fungsi Invers












Tasya hutabarat (hadir) buk
BalasHapus